Disponibilidade

O algoritmo Rapid Evolutionary Multi-objective Community Detection (re-mocd) está disponível como um projeto de código livre no GitHub, onde você pode escolher compilá-lo a partir do código-fonte ou usar a biblioteca pré-compilada a partir das releases. Ele também está disponível no PyPI do Python, permitindo instalação e uso de forma simples. Na data de publicação, a biblioteca possui 48 arquivos e 1.956 linhas de código. A biblioteca suporta dois modos de operação: via interface de linha de comando (CLI) ou por meio de chamadas diretas de funções utilizando a biblioteca PyPI.

Uso no PyPI

pip install re-mocd

Para a versão em Rust, será necessário construí-la a partir do código-fonte. As instruções para a construção podem ser encontradas no repositório oficial. A função run_rmocd pode ser chamada da seguinte forma:

import re_mocd
import networkx as nx

G nx.Graph([
   (0, 1), (0, 3), (0, 7),
   (1, 2), (1, 3), (1, 5), 
   (2, 3), 
   (3, 6), 
   (4, 5), 
   (4, 6), 
   (5, 6), 
   (7, 8)
   ])

partição = re_mocd.from_nx(G)

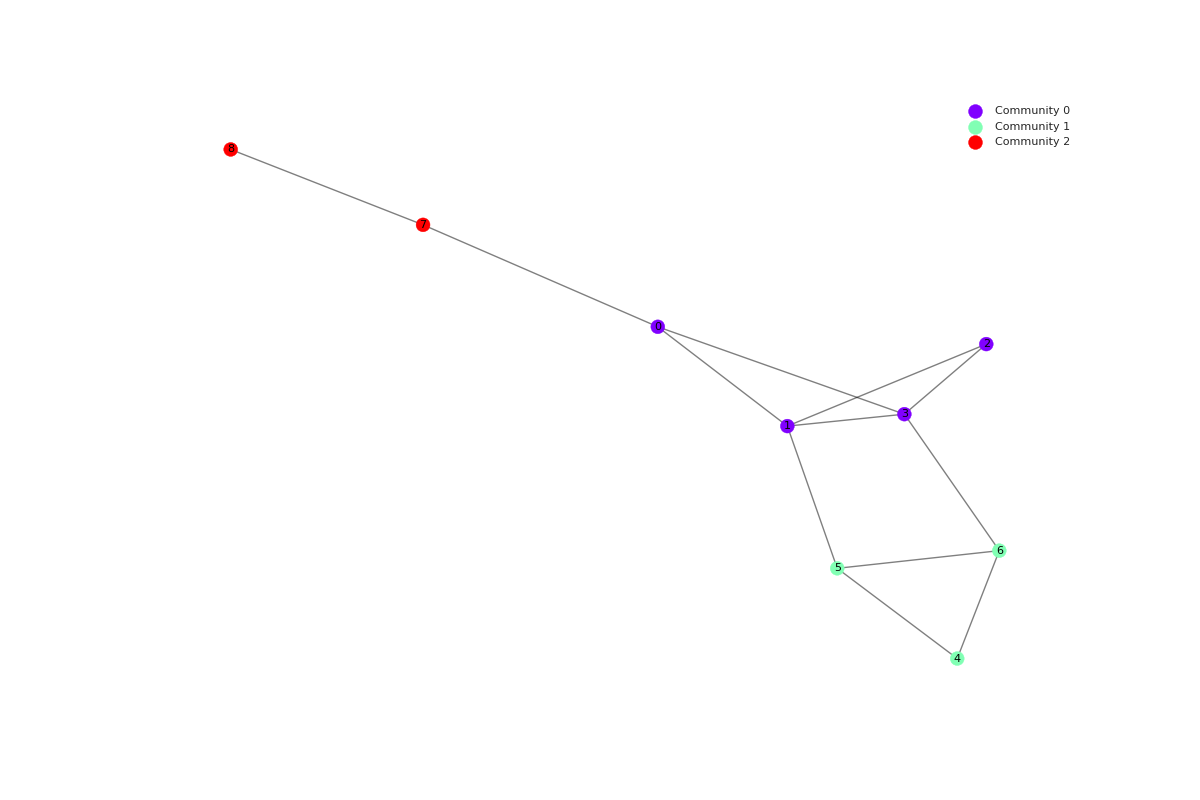
Dado o grafo acima definido pela biblioteca networkx, a função gerou a seguinte partição:

{0: 4, 1: 4, 2: 4, 3: 4, 4: 1, 5: 1, 6: 1, 7: 3, 8: 3}

Nesta representação, cada entrada corresponde a um par node:id, indicando a comunidade à qual cada nó pertence.

Modelo Matematico

Ao otimizar partições de grafos (ou detecção de comunidade), um objetivo comum é medir o quão “boa” é uma determinada partição. Em nossa implementação, calculamos duas métricas: uma que soma a comunidade interna ("intra") (ajustado para contagem dupla) e outra que usa os graus de nós pré-calculados para criar uma medida normalizada de conectividade entre uma comunidade e outras ("inter"), dada pela equaçao abaixo.

$$ Q(C) = \sum_{c \in C} \left[ \frac{|E(c)|}{m} - \left( \frac{\sum_{v \in c} \text{deg}(v)}{2m} \right)^2 \right], $$

Juntos, esses termos são combinados para produzir uma medida semelhante à modularidade (fixada entre –1 e 1). Mas o que isso significa em termos de desempenho? Vamos mergulhar nos detalhes.

Reorganizando a Partição em Comunidades

A primeira fase da nossa função reorganiza a partição—um mapeamento de cada nó para sua comunidade atribuída—em um hashmap que agrupa todos os nós por sua comunidade. Essa reorganização é direta: iteramos sobre cada nó na partição e adicionamos seu ID ao vetor correspondente.

• Tempo: Como processamos cada nó uma vez, esta etapa é $O(n)$, onde $n$ é o número de nós.
• Espaço: Um espaço extra de $O(n)$ é usado para armazenar esses grupos de comunidades.

Processando Cada Comunidade

Para cada comunidade, o algoritmo computa duas somas:

1. Arestas da Comunidade:
   Para cada nó em uma comunidade, iteramos sobre seus vizinhos. O detalhe importante aqui é que precisamos contar apenas as arestas cujos dois extremos pertencem à mesma comunidade. Para isso, realizamos uma busca binária no vetor de nós da comunidade.

   • Se um nó tem $d$ vizinhos e a comunidade tem $n₍c₎$ nós, cada busca binária custa $O(log n₍c₎)$.

   • Assim, para um nó, o custo é $O(d · log n₍c₎)$, e somando para todos os nós, o tempo total no pior caso será:

     $ O(m \cdot \log n) $ onde $m$ é o número total de arestas no grafo.

2. Grau da Comunidade e Medida Normalizada:
   Também recuperamos um grau precomputado para cada nó (de um hashmap, com custo médio $O(1)$ e atualizamos uma soma. Essa parte adiciona apenas uma sobrecarga constante por vizinho.

O tempo total para essa etapa é, portanto, dominado pela busca binária dentro da iteração dos vizinhos, resultando em um tempo de execução no pior caso de $O(m · log n)$.

Cálculo Final da Métrica

Depois que todas as comunidades são processadas (seja sequencialmente ou usando iteradores paralelos para melhorar o tempo de execução), a função calcula as métricas finais:

• Intra: Calculado como 1.0 menos a razão entre a soma das arestas intra‑comunidade e o número total de arestas.
• Modularidade: Computado como 1.0 menos a soma dos termos intra e inter, depois limitado ao intervalo [-1, 1].

Essa etapa envolve apenas algumas operações aritméticas, tornando-a essencialmente $O(1)$ em relação ao tamanho do grafo.

Complexidade Total

A complexidade total é a soma dos custos de construção das comunidades $O(n)$ e do processamento dos vizinhos $O(m · log n)$. Assim, a complexidade geral no pior caso é:

$ O(n + m \cdot \log n) $

Isso significa que, embora o algoritmo escale linearmente com o número de nós, o número de arestas (o fator mais pesado neste tipo de problema) é multiplicado por um fator logarítmico e continua eficiente para grafos esparsos.

Operadores Geneticos

Limitações dos Operadores Genéticos Tradicionais

Desafios do Crossover

A operação de crossover combina segmentos de duas soluções pais para produzir descendentes. Um método comumente utilizado, o crossover uniforme de dois pontos, é descrito da seguinte forma:

Escolhemos o crossover uniforme de dois pontos porque ele é imparcial em relação à ordem dos genes e pode gerar qualquer combinação de alelos a partir dos dois pais.

Embora seja versátil, essa abordagem é problemática para a detecção de comunidades devido aos seguintes motivos:

• Falta de percepção estrutural: Os pontos de crossover são escolhidos sem considerar a partição do grafo ou as propriedades estruturais.
• Degradação da qualidade: Os descendentes frequentemente não preservam as características das comunidades bem formadas, levando a soluções subótimas.

Desafios da Mutação

A mutação introduz pequenas mudanças aleatórias nas soluções para manter a diversidade genética. Na implementação tradicional¹ explica:

Na operação de mutação, selecionamos aleatoriamente alguns genes e os atribuímos a outros nós adjacentes selecionados aleatoriamente.

No entanto, essa abordagem apresenta várias desvantagens:

• Mudanças cegas ao contexto: Ignora o contexto mais amplo da solução, frequentemente perturbando a integridade estrutural da partição.
• Ineficácia aleatória: As mutações podem levar a soluções mal construídas, particularmente quando nós críticos para a estrutura da comunidade são alterados de forma indiscriminada.

Desafios da Inicialização

A população inicial estabelece a base para o progresso evolutivo. descreve o processo tradicional de inicialização:

No processo de inicialização, geramos indivíduos aleatoriamente. Para cada indivíduo, cada gene $g_i$ escolhe aleatoriamente um dos nós adjacentes ao nó $i$.

Os principais problemas incluem:

• Pontos de partida de baixa qualidade: Partições aleatórias provavelmente não refletem estruturas de comunidade significativas.
• Ineficácia na busca: Começar muito longe de soluções promissoras dificulta a convergência no vasto espaço de busca.

Operadores Genéticos Otimizados

Crossover Inteligente

• Garantimos que o segundo ponto nunca esteja muito próximo do primeiro, limitando a extensão do crossover e prevenindo mudanças estruturais drásticas, além de preservar relações chave entre as comunidades, garantindo que as comunidades não sejam divididas ou mescladas arbitrariamente.

Mutação Inteligente

• Um cache de frequência é construído para analisar as comunidades dos vizinhos de um nó antes de decidir sua atribuição.
• Após construir o mapa de frequência das comunidades dos vizinhos de um nó, a função seleciona a comunidade mais frequente.
• Os nós para mutação são selecionados com base em uma taxa de mutação controlada (0,3), diferente da proposta de 0,6.

Referencias